🟠 استخراج قانون دوم کپلر
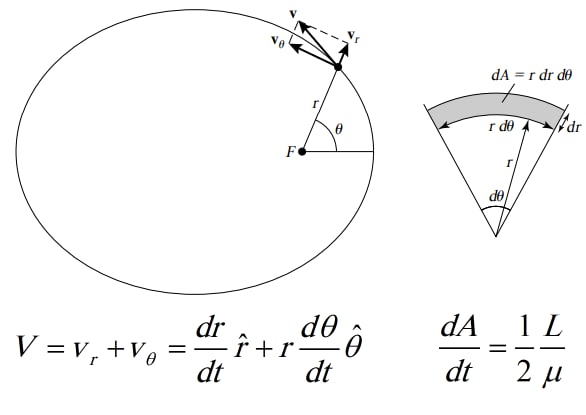
همانطور که در شکل اول تصویر نیز نشان داده شده است برای محاسبه مساحت بخش کوچکی از بیضی را که در بازه ی زمانی بسیار کوچکی طی می شود؛ به صورت زیر عمل می کنیم:
dA = dr(rdθ) = r dr dθ
اگر از کانون اصلی بیضی تا فاصله ی معین r مشتق بگیریم، مساحت جاروب شده در تغییرات بی نهایت کوچک θ، چنین می شود:
dA = (1/2)r^2 dθ
بنابراین آهنگ زمانی تغییر مساحت توسط خطی که از نقطه ای روی محیط بیضی ذبه کانون متصل می شود، برابر است با:
dA/dt = (1/2)r^2 (dθ/dt) *
حال سرعت مداری (V) را می توان با دو مولفه بیان کرد. یکی در امتداد r و دیگری عمود بر r. اگر r و θ را بردار های واحدی در امتداد r و عمود بر آن در نظر بگیریم(شکل دوم)، V را می توان چنین نوشت:
V = vr + vθ = (dr/dt)r + r(dθ/dt)θ
با جای گزینی vθ در معادله ی * خواهیم داشت:
dA/dt = (1/2)r vθ
چون r و vθ بر هم عمودند:
rvθ = I r × v I = I (L/μ) I = L/μ
و در آخر مشتق زمانی مساحت، قانون دوم کپلر را به دست می دهد:
dA/dt = L/2μ
قبلا ثابت شد که تکانه ی زاویه ای مدار ثابت است. بنابراین آهنگ تغییرات مساحت جاروب شده توسط خط واصل سیاره به کانون هم ثابت است.
🔸در این متن حروف bold شده نماد بردار می باشند.
🔺منبع: کتاب مقدمه ای بر اخترفیزیک نوین "بردلی کارول - دیل اوستلی"
🔘 بابت وقفه ای که در ارسال این پست به علت مشکلات اتصال به برنامه طی این چند هفته به وجود آمد عذر خواهی می کنم و امیدوارم دوباره شاهد این وقفه نباشیم.
🆔@physics3p
>>Click here to continue<<