Manim — замечательная библиотека для математических анимаций. С ее помощью создаю все свои видео. Если будет интересно, могу делиться наработками. Снизу — код, сверху — результат

from manim import *
import itertools as it


class Pyramid(ThreeDScene):
    def construct(self):
        a = 0.7  # длина стороны кубика
        n = 5  # высота пирамиды (в кубиках)

        pyramid = VGroup()
        for k, j, i in it.product(range(n), repeat=3):
            if (k + i < n) and (k + j < n):
                cube = Cube(a).set_fill(BLUE_D, opacity=1)
                cube.shift(a * np.array([i, -j, k]))
                pyramid.add(cube.set_stroke(WHITE, 1))
        self.set_camera_orientation(phi=PI/3, theta=-PI/3, focal_distance=500)
        self.play(Write(pyramid))
        self.wait()

— О библиотеке
— 200+ примеров кода
— Курс для новичков
— Курс для продвинутых

#manim

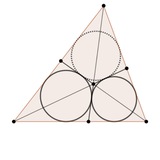
Всем привет! А вот смотрите какое красивое утверждение! Автором задачи является Виктор Тебо (Victor Thebault). Эта задача предлагалась читателям в журнале American Mathematical Monthly в 1952 году.

Требуется установить, что периметры треугольников PQR и KLM равны!

Доказать, что окружности касаются
RMM 2013 P3

🐾 🐶 Стипендия от Таксы Дуси

Такса Дуся и команда преподавателей Дабромат хотят сделать качественное образование доступным как можно большему числу школьников по всей России. Поэтому по традиции мы готовы взять учеников на стипендию от Таксы Дуси, которая покроет полную стоимость обучения на летних курсах по геометрии.

Для кого❓

— Стипендия предназначена для ребят НЕ из Москвы, не имеющих финансовой возможности заниматься на наших курсах, но сильно желающих.

— Мы ожидаем, что стипендиаты будут учиться хорошо. За плохую успеваемость следует отчисление с курсов.

Что нужно сделать для получения стипендии❓

Необходимо прислать на @dabromat_support следующую информацию:

— Мотивационное письмо

— Рекомендация от преподавателя

— Перечень самых значимых олимпиадных успехов за последние два учебных года

Дедлайн подачи заявления: 20 мая включительно.

Результаты отбора мы сообщим 25 мая.

Распространение приветствуется — пусть как можно больше школьников получат доступ к качественному системному обучению математике! 📨

В квадрате AM=BN. Доказать, что из трех отрезков, на которые поделена диагональ, можно сложить треугольник с углом 60°.

Докажите, что синие отрезки равны

Докажите, что сумма радиусов красного и синего кругов равна радиусу желтого.

Моя с Вовой Конышевым задача с 1 дня майский сборов.

Дан вписанный четырехугольник ABCD. Докажите, что существует окружность, касающаяся следующих пяти окружностей: описанной окружности четырехугольника ABCD, вписанных окружностей треугольников ABC и ABD, C-вневписанной окружности треугольника ACD и
D-вневписанной окружности треугольника BCD.

СПб отбор, 2004, 11 класс. Автор: Смирнов А.В.

ВсОШ 2002, финал, 11 класс. Автор: С.Л. Берлов

Правильное условие и картинка

Пусть ABCD —‍ вписанный четырёхугольник, O —‍ точка пересечения диагоналей AC‍ и BD.‍ Пусть окружности, описанные около треугольников ABO‍ и COD,‍ пересекаются в точке K.‍ Точка L‍ такова, что треугольник BLC‍ подобен треугольнику AKD.‍ Докажите, что если четырёхугольник BLCK‍ выпуклый, то он он является описанным.

Всем привет! К сожалению с чатом, привязанным к этому каналу не очень дальше получается. Будем считать, что это был неудачный эксперимент.

К счастью теперь есть много других геометрических групп, почти у все этих групп есть чаты - там вы всегда найдете с кем обсудить что-то геометрическое.

Синие прямые параллельны. Докажите, что пунктирные прямые проходят через центр красной окружности.

Часто ситуации, когда прямые можно "искривлять"
в коники, сохраняя дважды касание,
объясняются таким соображением:

Лемма (пучок, дважды касающемя сокружности в данных точках,
или обобщенная директриса для окружности и прямой).

Пусть коника $\omega = 0$ пересекает прямую $l=0$ в точках $A$ и $B$. Тогда коники, касающиеся $\omega = 0$ в точках $A$ и $B$ --- это пучок $\omega + \lambda l^2 = 0$.
(если $\omega$ --- окружность, то тут написано гмт $X$, для которых отношение $pow (X, \omega)$ к расстоянию от $X$ до $l$ равно const )

=========

Из этого утверждение следует в одну строчку:
Скажем, у нас пересекаются эллипсы $\omega + \lambda_1 l_1^2 = 0$ и
$\omega + \lambda_2 l_2^2 = 0$. Через точки их пересечения проходит вырожденная коника (пара прямых) $\lambda_1 l_1^2 - \lambda_2 l_1^2 = 0= 0$, которая, очевидно, проходит через
точку пересечения прямых $l_1=0$ и $l_2=0$.

=============

Еще о применении этого - напр. в последнем упражнении 17 статьи
https://www.mathnet.ru/links/be697473b64d836385257c3b19ae4332/kvant4535.pdf

============

Еще и еще ... - например, быстро решается задача Ф. Нилова
о параболическом 4-угольнике
https://www.mathnet.ru/links/c637ed850ac5245f76ddfe68fb2d9b99/mp254.pdf
Так:
Пусть $\omega = x^2+y^2-1$.
То, что $\omega - l_1^2 = 0$ --- параболического типа, задается условием $a_1^2+b^1=1$, где $l_1 = a_1x+b_1y+c_1$.
Аналогично для $l_2$. И отсюда получаем, что наша вырожденная коника (= пара диагоналей параболического 4-ка) $l_1^2-l_2^2 = 0$ --- это пара ортогональных прямых.

теорема о шести окружностях

Про треугольную цепочку из шести окружностей можно прочитать в статье из Математического просвещения
"Теорема о семи окружностях и другие новые теоремы"

Докажите, что если два прямоугольных параллелепипеда имеют равные объёмы, то их можно расположить в пространстве так, что любая горизонтальная плоскость, пересекающая один из них, будет пересекать и второй, причём по многоугольнику той же площади.

ВсОШ-1993, 11.8. Автор: Терешин Д.А.

Один из способов увидеть, что R не меньше 2r в треугольнике, это посчитать расстояние от центра описанной окружности до точки Нагеля.