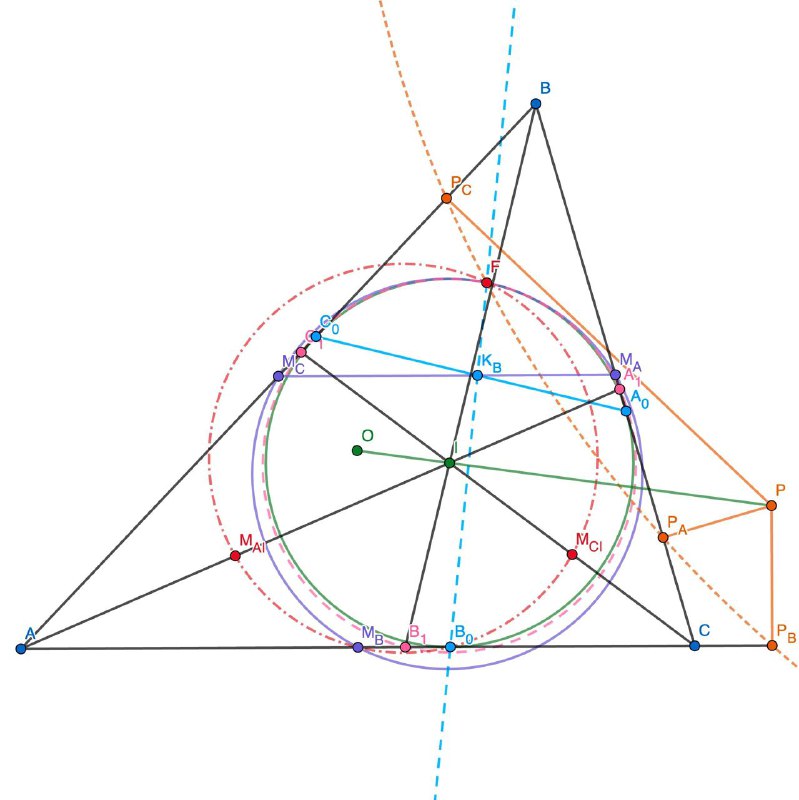
№20 (Вспоминаем точку Фейербаха)
Дан треугольник ABC
O - центр описанной окружности
I - центр вписанной окружности
A_0, B_0, C_0 - точки касания вписанной окружности со сторонами.
A_1, B_1, C_1 - основания биссектрис.
M_A, M_B, M_C - середины сторон.
P - точка на прямой OI, P_A, P_B, P_C - основания перпендикуляров из P на стороны треугольника.
K_B - точка пересечения M_A M_C и A_0 C_0. Аналогично определяются K_A и K_B.
M_AI, M_BI, M_CI - середины AI, BI, CI соответственно
Доказать, что:
a) (M_A M_B M_C) касается (A_0 B_0 C_0) (точка Фейербаха)
b) Точка Фейербаха лежит на прямой B_0 K_B
c) Точка Фейербаха лежит на окружности (A_1, B_1, C_1) (теорема Емельяновых)
d) Точка Фейербаха лежит на окружности (P_A, P_B, P_C) (теорема Фонтене)
e) Точка Фейербаха лежит на окружности (B_0, M_AI, M_CI)
f) Попробуйте сформулировать аналогичные утверждения, но для вневписанной окружности
https://geogebra.org/m/n2ejddyd
>>Click here to continue<<