Channel: скучні задачі
а тепер така нормальна по обсягу добірка на трикутник a=(b²+c²)/(b+c)
1. жергоніана і симедіана співпадають
2. триполяра інцентра паралельна симедіані
3. точка фейєрбаха лежить на медіані
4. X(7)X(8) || BC
5. OI ⊥ жергоніані
6. описаний еліпс з центром X(9) проходить через перетин медіани з (ABC)
7. точка дотику напівзовнівписаного кола - фокус вписаної параболи з директорисою X(4)X(8)
8. середина дуги BC - фокус вписаної параболи з директорисою X(4)X(9)
9. пряма із вершини A через точку шиффлера проходить через точку штейнера
1. жергоніана і симедіана співпадають
2. триполяра інцентра паралельна симедіані
3. точка фейєрбаха лежить на медіані
4. X(7)X(8) || BC
5. OI ⊥ жергоніані
6. описаний еліпс з центром X(9) проходить через перетин медіани з (ABC)
7. точка дотику напівзовнівписаного кола - фокус вписаної параболи з директорисою X(4)X(8)
8. середина дуги BC - фокус вписаної параболи з директорисою X(4)X(9)
9. пряма із вершини A через точку шиффлера проходить через точку штейнера
❤2🔥1🤯1
скучні задачі
а тепер така нормальна по обсягу добірка на трикутник a=(b²+c²)/(b+c) 1. жергоніана і симедіана співпадають 2. триполяра інцентра паралельна симедіані 3. точка фейєрбаха лежить на медіані 4. X(7)X(8) || BC 5. OI ⊥ жергоніані 6. описаний еліпс з центром X(9)…
на основі 7-8, но вже для різницевого трикутника
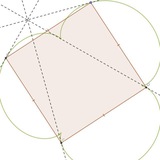
дано трикутник ABC і вписану коніку з фокусами P, Q. трикутники APQ, BPQ, CPQ доповнили до гармонійних чотирикутників точками A', B', C'.
а) доведіть перспективність ABC і A'B'C'
б) доведіть що перспектор X цих трикутників належить колу (A'B'C')
а) доведіть перспективність ABC і A'B'C'
б) доведіть що перспектор X цих трикутників належить колу (A'B'C')
🔥3
задача від @mamonovclhgffkuffhj
(!) існує коло що дотикається до описаного і гіперболи жерабека і проходить через ортоцентр і центр описаного кола
(!) існує коло що дотикається до описаного і гіперболи жерабека і проходить через ортоцентр і центр описаного кола
❤3
скучні задачі
задача від @mamonovclhgffkuffhj (!) існує коло що дотикається до описаного і гіперболи жерабека і проходить через ортоцентр і центр описаного кола
ну і ось лема за тим же авторством, яку я згадав в коментарях.
сині точки P, Q ізогональні. через них і вершини проведено коніку (ABCPQ), точка перетину U якої з описаним колом (ABC), що відрізняється від вершин. через U провели довільну пряму, яка перетинає (ABC) в R і (ABCPQ) в S.
(!) доведіть вписаність чотирикутника PQRS
сині точки P, Q ізогональні. через них і вершини проведено коніку (ABCPQ), точка перетину U якої з описаним колом (ABC), що відрізняється від вершин. через U провели довільну пряму, яка перетинає (ABC) в R і (ABCPQ) в S.
(!) доведіть вписаність чотирикутника PQRS
HTML Embed Code: